모델이 훈련데이터에 과하게 맞추는 과대적합을 줄이고, 일반화 성능을 높이기
큰 계수에 패널티 줘서 모델 복잡도 낮춤

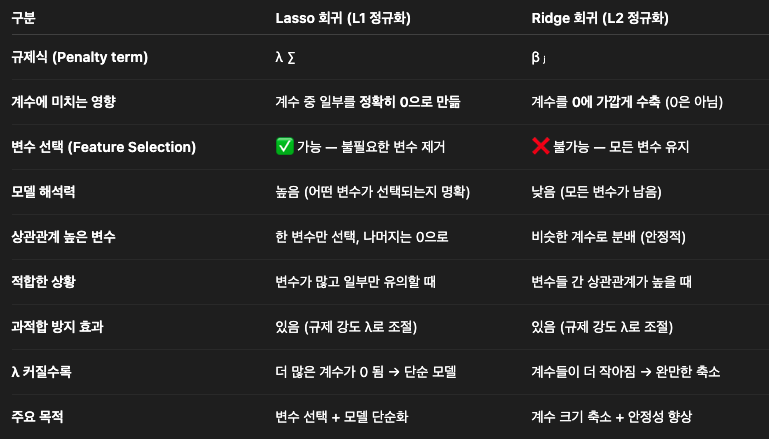
Lasso(L1)
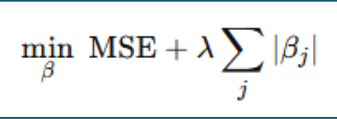
선형회귀에 “규제항(Regularization term)”을 추가한 모델
기본 선형회귀는 MSE(평균제곱오차) 를 최소화하지만, Lasso는 거기에 더해 회귀계수의 절댓값 합(∑|βᵢ|) 도 최소화
MSE를 최소화 (예측 잘하게)
β들의 절댓값 합도 최소화 (모델 단순하게)
규제가 강하면(λ↑), 일부 회귀계수(β)가 정확히 0이 됨 → 즉, 해당 변수는 모델에서 완전히 제외됨
불필요한 변수 자동 제거 (Feature Selection)
장점
변수 선택이 자동으로 이루어짐
모델에서 가장 중요한 특성이 무엇인지 알게 되는 등 모델 해석력이 좋아짐
단점
변수간 상관관계가 높으면 성능이 떨어짐
Ridge(L2)

회귀계수를 0으로 보내는 대신, 0에 가까워지도록 ‘부드럽게’ 수축 → 즉, β 값들을 너무 크게 만드는 걸 방지함(Overfitting 방지)
하지만 완전히 0으로 만들지는 않음. Lasso처럼 변수 제거(Feature Selection)는 불가능
λ를 크게 하면 → 패널티가 커지고 → 계수들이 더 작아짐 → 단순한 모델
λ를 작게 하면 → 일반 회귀(OLS)에 가까워짐
장점: 변수 간 상관관계가 높을 때 안정적
단점: 불필요한 변수 제거 못함
Elastic Net (L1 + L2 혼합)
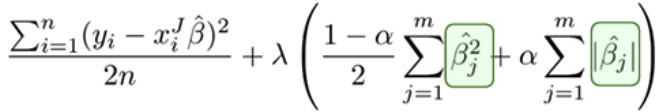
변수 선택 가능, 변수 간 상관관계를 반영한 정규화
피처 수가 많고, 상관 피처 묶음이 있으며, 일부는 0이길 원할 때.

위의 3가지 성능 비교 예제
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import RidgeCV, LassoCV, ElasticNetCV
from sklearn.pipeline import Pipeline
from sklearn.metrics import r2_score, mean_squared_error
# 1. 데이터 준비
df = sns.load_dataset("mpg").dropna().copy()
# 숫자형만 사용하고, 타깃 mpg는 분리
X = df.select_dtypes(include=["float64", "int64"]).drop(columns=["mpg"])
y = df["mpg"]
x_tr, x_te, y_tr, y_te = train_test_split(
X, y, test_size=0.2, random_state=42
)
# 2. Ridge 모델
ridge_pipe = Pipeline([
("scaler", StandardScaler()),
("ridge", RidgeCV(alphas=[0.1, 1.0, 10.0, 100.0], cv=5))
])
ridge_pipe.fit(x_tr, y_tr)
y_pred_ridge = ridge_pipe.predict(x_te)
# 3. Lasso 모델
lasso_pipe = Pipeline([
("scaler", StandardScaler()),
("lasso", LassoCV(alphas=[0.001, 0.01, 0.1, 1.0, 10.0],
cv=5,
max_iter=5000))
])
lasso_pipe.fit(x_tr, y_tr)
y_pred_lasso = lasso_pipe.predict(x_te)
# 4. Elastic Net 모델
# l1_ratio는 L1과 L2 비율 (1이면 Lasso에 가까움, 0이면 Ridge에 가까움)
enet_pipe = Pipeline([
("scaler", StandardScaler()),
("enet", ElasticNetCV(
l1_ratio=[0.2, 0.5, 0.8, 0.9, 1.0], # 여러 비율 테스트
alphas=[0.001, 0.01, 0.1, 1.0, 10.0], # 규제 세기
cv=5,
max_iter=5000
))
])
enet_pipe.fit(x_tr, y_tr)
y_pred_enet = enet_pipe.predict(x_te)
# 5. 평가 함수
def metrics(y_true, y_pred):
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
return {
"R2": r2_score(y_true, y_pred),
"MSE": mse,
"RMSE": rmse
}
print("Ridge :", metrics(y_te, y_pred_ridge))
print("Lasso :", metrics(y_te, y_pred_lasso))
print("ElasticNet :", metrics(y_te, y_pred_enet))
# 6. 계수 비교
ridge_coef = ridge_pipe.named_steps["ridge"].coef_
lasso_coef = lasso_pipe.named_steps["lasso"].coef_
enet_coef = enet_pipe.named_steps["enet"].coef_
coef_df = pd.DataFrame({
"feature": X.columns,
"Ridge": ridge_coef,
"Lasso": lasso_coef,
"ElasticNet": enet_coef
})
print("\n계수 비교")
print(coef_df)
=========================================================
# mpg 회귀: (1) 선형성 검증(잔차 vs 각 피처)
# (2) 다항식은 horsepower, weight만 2차/교차항 추가
# =========================================================
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler, OneHotEncoder
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
# 1) 데이터 로드 및 피처 선택
df = sns.load_dataset("mpg")
# 사용할 컬럼 정의
poly_cols = ["horsepower", "weight"] # 다항식(2차) 적용 대상
num_all = ["horsepower", "weight", "acceleration", "displacement", "cylinders", "model_year"]
cat_cols = ["origin"] # 범주형(원-핫)
use_cols = ["mpg"] + num_all + cat_cols
# 결측 제거
df = df[use_cols].dropna()
X = df[num_all + cat_cols]
y = df["mpg"]
# 학습/평가 분리
X_tr, X_te, y_tr, y_te = train_test_split(X, y, test_size=0.2, random_state=42)
# ---------------------------------------------------------
# A) 베이스라인: 순수 선형(모든 피처 선형), 스케일은 수치형만
# ---------------------------------------------------------
num_rest = [c for c in num_all] # 전 수치형을 선형으로 사용
num_linear_transformer = Pipeline([
("scaler", StandardScaler())
])
cat_transformer = OneHotEncoder(handle_unknown="ignore", sparse_output=False)
preprocess_linear = ColumnTransformer(
transformers=[
("num", num_linear_transformer, num_rest), # 수치형만 표준화
("cat", cat_transformer, cat_cols), # 범주형 원-핫
],
remainder="drop",
)
pipe_linear = Pipeline([
("prep", preprocess_linear),
("model", LinearRegression())
])
pipe_linear.fit(X_tr, y_tr)
# (선형성 검증) 훈련셋 잔차 계산
y_tr_pred_lin = pipe_linear.predict(X_tr)
resid_lin = y_tr - y_tr_pred_lin
# (성능) 테스트셋
y_te_pred_lin = pipe_linear.predict(X_te)
r2_lin = r2_score(y_te, y_te_pred_lin)
mae_lin = mean_absolute_error(y_te, y_te_pred_lin)
rmse_lin = np.sqrt(mean_squared_error(y_te, y_te_pred_lin))
print("=== [Linear] Test 성능 ===")
print(f"R² : {r2_lin:.4f}")
print(f"MAE : {mae_lin:.4f}")
print(f"RMSE : {rmse_lin:.4f}")
fig, axes = plt.subplots(1, 2, figsize=(10, 4), sharey=True)
for ax, col in zip(axes, ["horsepower", "weight"]):
ax.scatter(X_tr[col], resid_lin, alpha=0.6)
ax.axhline(0, linestyle="--")
ax.set_xlabel(col)
ax.set_title(f"Residuals vs {col} (Linear baseline)")
axes[0].set_ylabel("Residuals")
plt.tight_layout()
plt.show()
plt.figure(figsize=(6,4))
plt.scatter(y_tr_pred_lin, resid_lin,alpha=0.6)
plt.axhline(0, linestyle="--")
plt.title("Residuals vs Predict (Linear baseline)")
plt.xlabel("Predict")
plt.ylabel("Residuals")
plt.tight_layout()
plt.show()
# ---------------------------------------------------------
# B) 다항 모델: horsepower, weight만 2차 + 교차항, 나머지는 선형
# - poly_cols -> PolynomialFeatures(deg=2)
# - 다른 수치형/범주형은 베이스와 동일
# ---------------------------------------------------------
poly_transformer = Pipeline([
("poly", PolynomialFeatures(degree=2, include_bias=False)), # [hp, wt, hp^2, hp*wt, wt^2]
("scaler", StandardScaler())
])
num_rest_no_poly = [c for c in num_all if c not in poly_cols] # 다항 미적용 수치형
num_rest_transformer = Pipeline([
("scaler", StandardScaler())
])
preprocess_poly = ColumnTransformer(
transformers=[
("polyNum", poly_transformer, poly_cols), # hp, wt만 다항+스케일
("numRest", num_rest_transformer, num_rest_no_poly), # 나머지 수치형 스케일
("cat", cat_transformer, cat_cols), # 범주형 원-핫
],
remainder="drop",
)
pipe_poly = Pipeline([
("prep", preprocess_poly),
("model", LinearRegression())
])
pipe_poly.fit(X_tr, y_tr)
# (선형성 검증) 훈련셋 잔차 계산
y_tr_pred_poly = pipe_poly.predict(X_tr)
resid_poly = y_tr - y_tr_pred_poly
# (성능) 테스트셋
y_te_pred_poly = pipe_poly.predict(X_te)
r2_poly = r2_score(y_te, y_te_pred_poly)
mae_poly = mean_absolute_error(y_te, y_te_pred_poly)
rmse_poly = np.sqrt(mean_squared_error(y_te, y_te_pred_poly))
print("\n=== [Polynomial on hp, wt only] Test 성능 ===")
print(f"R² : {r2_poly:.4f}")
print(f"MAE : {mae_poly:.4f}")
print(f"RMSE : {rmse_poly:.4f}")
# ---------------------------------------------------------
# C) 성능 비교표
# ---------------------------------------------------------
comp = pd.DataFrame({
"Model": ["Linear (all features linear)",
"Poly(deg=2) on [horsepower, weight]"],
"R2": [r2_lin, r2_poly],
"MAE": [mae_lin, mae_poly],
"RMSE": [rmse_lin, rmse_poly]
})
print("\n=== 성능 비교 (Test) ===")
print(comp)
# ---------------------------------------------------------
# D) 선형성 검증: 잔차 vs 각 피처(훈련셋, 베이스라인 잔차 기준)
# - 잔차가 0 주변에 무작위면 선형성 OK
# - 곡률(U/∩) 보이면 해당 피처에 다항/변환 고려
# ---------------------------------------------------------
fig, axes = plt.subplots(1, 2, figsize=(10, 4), sharey=True)
for ax, col in zip(axes, ["horsepower", "weight"]):
ax.scatter(X_tr[col], resid_poly, alpha=0.6)
ax.axhline(0, linestyle="--")
ax.set_xlabel(col)
ax.set_title(f"Residuals vs {col} (Linear poly)")
axes[0].set_ylabel("Residuals")
plt.tight_layout()
plt.show()
plt.figure(figsize=(6,4))
plt.scatter(y_tr_pred_poly, resid_poly, alpha=0.6)
plt.axhline(0, linestyle="--")
plt.title("Residuals vs Predict (Linear Poly)")
plt.xlabel("Predict")
plt.ylabel("Residuals")
plt.tight_layout()
plt.show()'데이터 분석 > 머신러닝, 딥러닝' 카테고리의 다른 글
| 딥러닝 (0) | 2025.11.14 |
|---|---|
| 시계열 데이터 (0) | 2025.11.13 |
| 회귀 분석(Regression Analysis) (0) | 2025.11.10 |
| Gradient Boosting (0) | 2025.11.07 |
| RandomForest까지의 종합적 예제 (0) | 2025.11.06 |